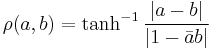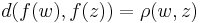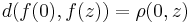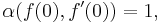Complex geodesic

In mathematics, a complex geodesic is a generalization of the notion of geodesic to complex spaces.

Definition

Let (X, || ||) be a complex Banach space and let B be the open unit ball in X. Let Δ denote the open unit disc in the complex plane C, thought of as the Poincaré disc model for 2-dimensional real/1-dimensional complex hyperbolic geometry. Let the Poincaré metric ρ on Δ be given by

$\rho (a, b) = \tanh^{-1} \frac{| a - b |}{|1 - \bar{a} b |}$

and denote the corresponding Carathéodory metric on B by d. Then a holomorphic function f : Δ → B is said to be a complex geodesic if

$d(f(w), f(z)) = \rho (w, z) \,$

for all points w and z in Δ.

Given u ∈ X with ||u|| = 1, the map f : Δ → B given by f(z) = zu is a complex geodesic.
Geodesics can be reparametrized: if f is a complex geodesic and g ∈ Aut(Δ) is a bi-holomorphic automorphism of the disc Δ, then f o g is also a complex geodesic. In fact, any complex geodesic f₁ with the same image as f (i.e., f₁(Δ) = f(Δ)) arises as such a reparametrization of f.
If

$d(f(0), f(z)) = \rho (0, z)$

for some z ≠ 0, then f is a complex geodesic.

$\alpha (f(0), f'(0)) = 1,$

where α denotes the Caratheodory length of a tangent vector, then f is a complex geodesic.

Earle, Clifford J. and Harris, Lawrence A. and Hubbard, John H. and Mitra, Sudeb (2003). "Schwarz's lemma and the Kobayashi and Carathéodory pseudometrics on complex Banach manifolds". In Komori, Y., Markovic, V. and Series, C. (eds). Kleinian groups and hyperbolic 3-manifolds (Warwick, 2001). London Math. Soc. Lecture Note Ser. 299. Cambridge: Cambridge Univ. Press. pp. 363–384.